Prisoner’s Looping Strategy in Python

Veritasium recently uploaded a fantastic explanation of this strategy here:

https://www.youtube.com/watch?v=iSNsgj1OCLA

The basis of this problem is that there are 100 prisoners. The prisoners are taken to a room with 100 boxes each containing a random prisoners’ ID within them.
The (clearly maniacle) prison guards say that:

• Each prisoner is to open no more than 50 boxes to find their number
• If every prisoner finds the box which contains their number, they are all set free
• If even one prisoner fails to find their box, they are all executed
• They are allowed to strategise beforehand but must complete the task one-by-one.

So the solution to this problem, is to increase the probability as much as possible that every prisoner will find their number. If every prisoner were to search randomly, the probability is 50% (for each prisoner) and overall it becomes 1/2 * 1/2 * 1/2 .. and so on. Basically, practically impossible.

The solution dictates that each prisoner must start with the box that has their number (ID) on it, and follow the id contained in it to the next box. Since there is a finite system, the numbers contained in the box form a closed cycle (loop) in any n amount. Imagine these boxes as key, value pairs in which the value refers to the direction in a network. For example, if a prisoner opens box 23 and it has id 12 contained within it, he then goes to box 12 and finds id 45 in it, goes to box 45 and finds id 10 in it.. and so forth.

import random
from collections import defaultdict
import networkx as nx
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt

#define prisoners and boxes
prisoners = [*range(1,101,1)]
box_num = [*range(1,101,1)]

#randomly put ID slips in each box
random.shuffle(prisoners)
for box in box_num:
    boxes[box] = prisoners[box -1]

So in setting up the situation we’ve defined prisoners, defined boxes, and randomly shuffled IDs into the 100 boxes.

We want to test the theory that the id, box pairs exist in a closed loop. If we try it a couple of times and graph the output using networkx:

G = nx.DiGraph()
G.add_edges_from(boxes.items())
c = nx.recursive_simple_cycles(G)

nx.draw_networkx(G)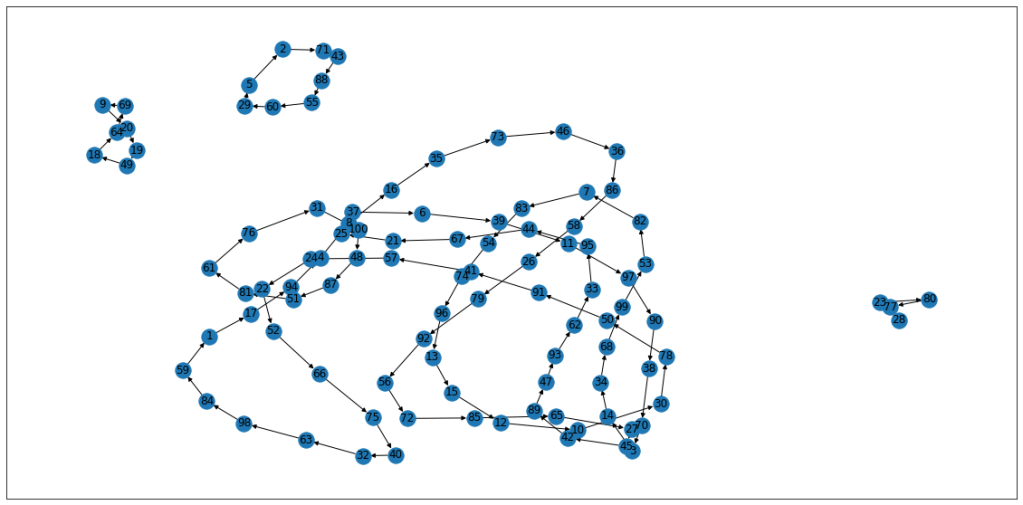

You can see for example, prisoner no. 2, following this strategy, would get back to his ID within the requisite 50 tries. Any ID on the larger loop, would not get back to their ID within the maximum tries.

Again, the IDs on the right form a loop of less than 50, so anyone following that strategy would eventually find their ID. We also have a loop of 1 for ID 51 in this iteration.

If you think about it, the overall probablity of success is directly linked to the chance that all “loops” are less than 50 long. That way if everyone followed the loop, everyone would be successful. We know that this happens about 30% of the time, so the overall probablity of success is 30%.

So we now want to test out the stragety by simulating each prisoner searching for their

#If we set default to true, and then switch it when a prisoner lands on a cycle longer than 50, it fails everybody.
overall_success = "Success"

#simulating prisoners by checking the length of the loop that they exist on. If it's too long, success = false.
for prisoner in prisoners:
found = False
    for c in cycles:
        if(prisoner in c):
            if(len(c) > 50): overall_success = "Unsuccessful"

If I run this 10 times, I get a mixture of successful and unsuccessful attempts.

There is 50/50 successful/unsuccessful in there, which isn’t representative of the overall probability. So let’s run it lots of times and see what the overall outcomes come out to.

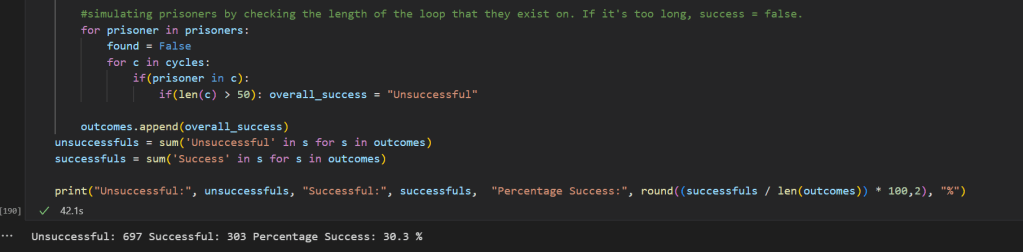
As you can see this is now representative of the probability of success. Full code is below which has the entire block in it:

import random
from collections import defaultdict
import networkx as nx
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
from collections import Counter


outcomes = []
for i in range(0,1000,1):
    prisoners = [*range(1,101,1)]
    box_num = [*range(1,101,1)]

    boxes = {}

    random.shuffle(prisoners)

    for box in box_num:
        boxes[box] = prisoners[box -1]

    G = nx.DiGraph()
    G.add_edges_from(boxes.items())


    c = nx.recursive_simple_cycles(G)
    #plt.figure(figsize=(20,10)) 
    #nx.draw_networkx(G)

    cycles = sorted(c)

    #If we set default to true, and then switch it when a prisoner lands on a cycle longer than 50, it fails everybody.
    overall_success = "Success"

    #simulating prisoners by checking the length of the loop that they exist on. If it's too long, success = false.
    for prisoner in prisoners:
        found = False
        for c in cycles:
            if(prisoner in c):
                if(len(c) > 50): overall_success = "Unsuccessful"

    outcomes.append(overall_success)
unsuccessfuls = sum('Unsuccessful' in s for s in outcomes)
successfuls = sum('Success' in s for s in outcomes)
  
print("Unsuccessful:", unsuccessfuls, "Successful:", successfuls,  "Percentage Success:", round((successfuls / len(outcomes)) * 100,2), "%")

Also available over on GitHub: https://github.com/nzjp1/prisoners_loop_strategy_python/